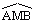 et
et 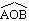 .
.
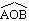 mesure 180° alors
l'angle inscrit
mesure 180° alors
l'angle inscrit 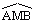 mesure environ 90°. En fait, l'angle
mesure environ 90°. En fait, l'angle 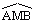 mesure exactement 90°.
mesure exactement 90°. Il faut donc prouver que
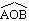 = 2
= 2 
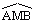
 |
Compléter
les phrases suivantes en utilisant les mots "au centre", "arc" ou
"inscrit": |
||
L'objectif
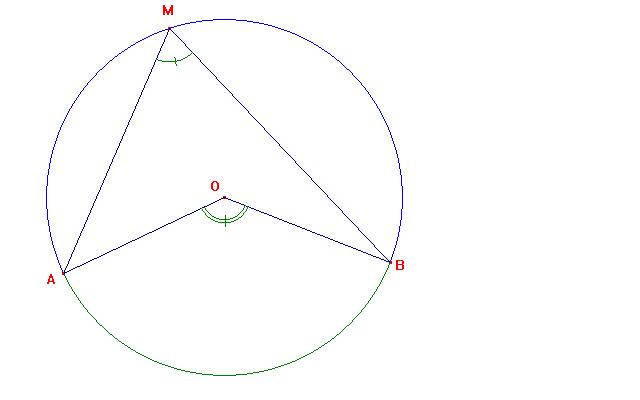
de l'exercice suivant est de découvrir une relation entre les angles 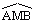 et et 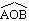 . .
|
|||
| Nous allons nous intéresser
maintenant au dessin ci-contre où la mesure de chaque angle apparaît: |
|||
| Pour résumer: si dans un cercle, un angle inscrit et un angle au centre interceptent le même arc alors l'angle au centre semble être le double de l'angle inscrit. | |||
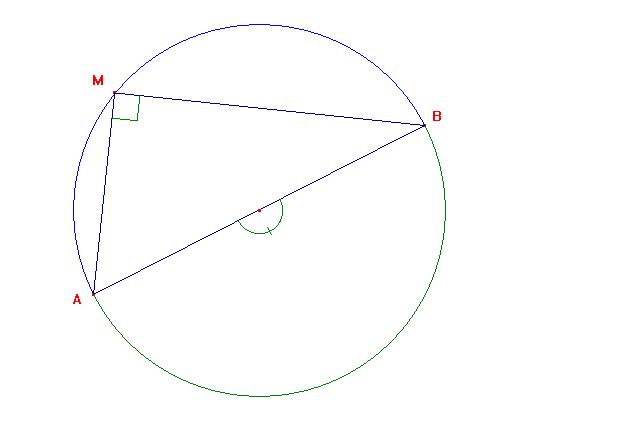
Cas particulier:  |
Si l'angle au centre 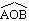 mesure 180° alors
l'angle inscrit mesure 180° alors
l'angle inscrit 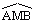 mesure environ 90°. En fait, l'angle
mesure environ 90°. En fait, l'angle 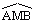 mesure exactement 90°. mesure exactement 90°. |
||
| C'est une propriété vue en 4ème, laquelle ? | |||
| Nous
pouvons alors énoncer la conjecture suivante: si dans un
cercle, un angle inscrit et un angle au centre interceptent le même arc
alors l'angle au centre est le double de l'angle inscrit". Il faut donc prouver que 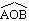 = 2
= 2  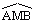 |
|||